Soustava 2 rovnic o 2 neznámých

Dvě rovnice o dvou neznámých můžeme řešit několika matodami. Jedná se zejména o metodu dosazovací, sčítací a grafickou metodu.

DOSAZOVACÍ METODA

Postup řešení:

1. Vybereme si jedno písmeno (neznámou) a vyjádříme si jej z jedné rovnice. (Vybíráme tak, aby u písmene buď nebylo napsané žádné číslo - čili 1, a nebo číslo, se kterým se lépe počítá/dělí - např. 2, 4, 5, 10...)
   
2. Výsledek vyjádření dosadíme do druhé rovnice místo tohoto písmene (neznámé).
3. Získáme rovnici o jedné neznámé, kterou vyřešíme.
4. Výsledek dosadíme zpět do původní vyjádřené rovnice a vypočítáme hodnotu zbývajícího písmene (neznámé).

Př. 1:

Př. 2:

Př. 3:

Př. 4:

Videonávod pro řešení:

SČÍTACÍ METODA

Postup řešení:

1. Vybereme si jedno písmeno (neznámou) a zkontrolujeme jaké znaménko a číslo se u něj nachází.
   
2. Pokud u neznámé nemáme stejné číslo s různým znaménkem, vynásobíme rovnice tak, abychom získali stejné číslo (společný násobek)  s opačným znaménkem.
3. Sečteme upravené rovnice. Vybrané písmeno (neznámá) se odečte (zmizí).
4. Řešíme rovnici o jedné neznámé. Výsledek této rovnice dosadíme do jedné z rovnic a vypočítáme.

Př. 5:

Př. 6:

Př. 7:

Př. 8:

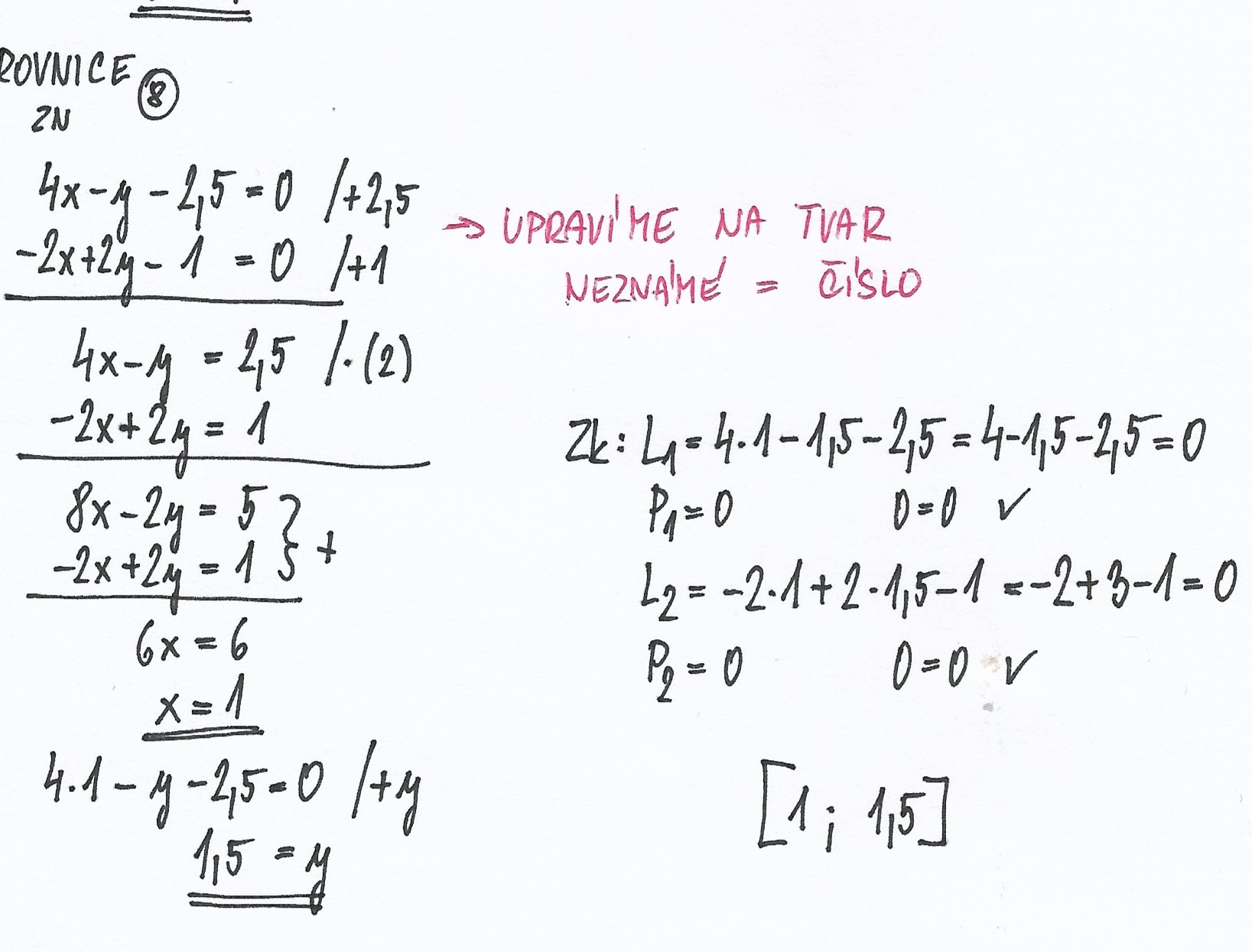
Př. 9:

Videonávod pro řešení:

Příklady na procvičení:

1) x + 2y = - 4 

    2x - 3y = 13                          

2) 2u + 5v = 19 

     u - v = 6                      

3) c + 2d = 7

   3c - 4d = - 29                                  

4) 2e + 3f = 7

    e - 7f = - 1

5) 5x + 5y = 0    

  - 3x + 5y = 8                        

6) 5a - b = - 20

   3a + 2b = - 12                      

7) 3y - 2x = 35

  6x + 8y = - 20                              

8) 5x + 14 = 2y + 8

   3x + 4y = - 14

9) 3a + 5 = 3b + 6

     2a + 2 = 5 - b - 2a                   

10) 3x - 2y = 10(x + y)

     12x + 2y = 13                

11) 2(x - 7) + 4(y + 2) = - 20 

 3(2x + 5) + 2(3y + 4) = 11           

12) 5(a +b) - (b - a) = 15

    2(a - b) + 4b + a = 7