Násobení mnohočlenů

Násobení jednočlenů

Jednočleny násobíme tak, že násobíme čísla s čísly a stejná písmena se stejnými písmeny (jejich exponenty sčítáme).

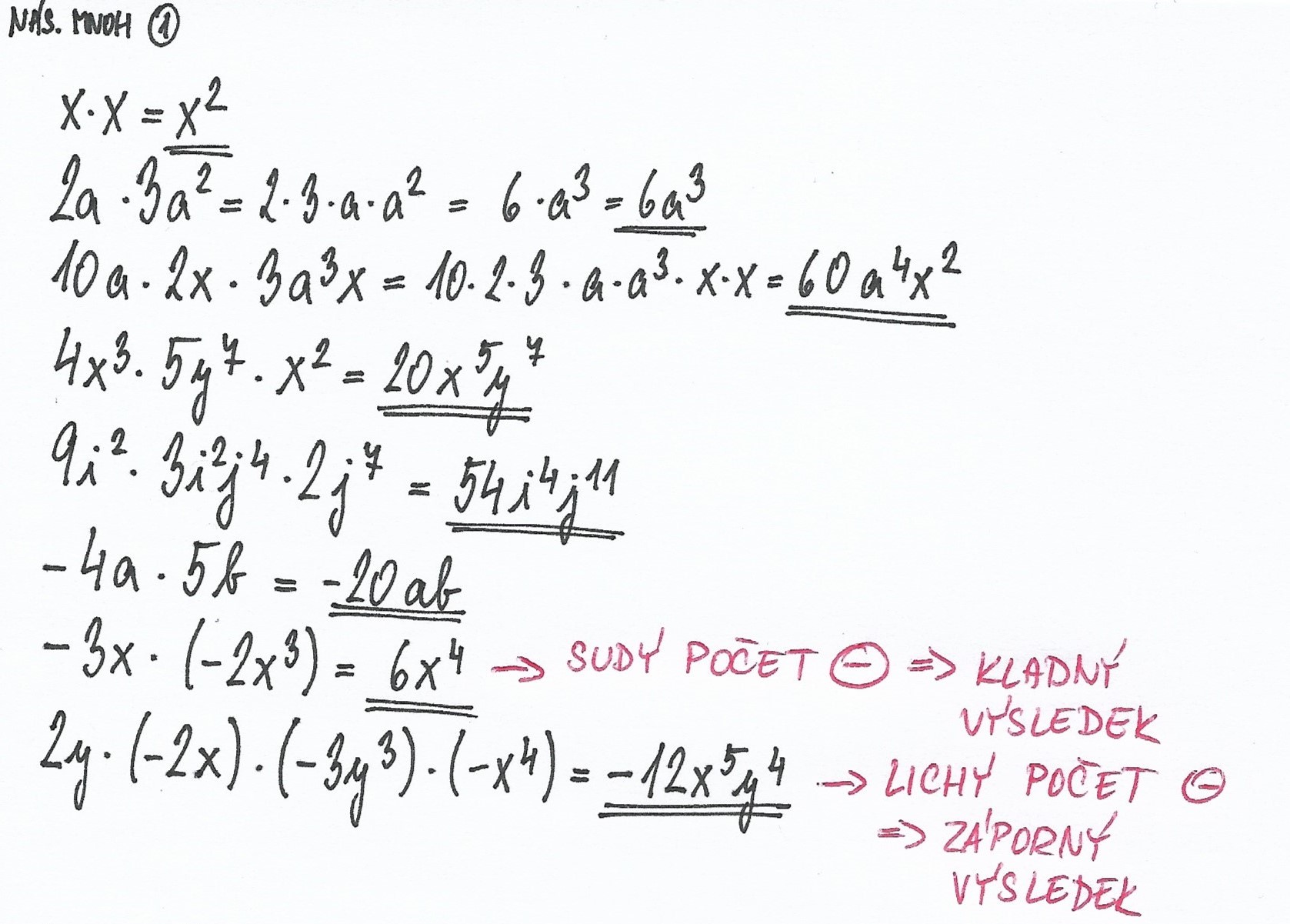
Násobení jednočlenu a mnohočlenu

Mnohočlen vynásobíme tak, že každý člen mnohočlenu vynásobíme jednočlenem.

Násobení mnohočlenu mnohočlenem

Tyto mnohočleny vynásobíme tak, že každý člen prvního mnohočlenu vynásobíme s každým členem druhého mnohočlenu. ("každý s každým")

Násobení mnohočlenů pomocí vzorců

(A + B)² = A² + 2AB + B²

(A - B)² = A² - 2AB + B²

(A + B) . (A - B) = A² - B²

Videonávody pro počítání:

Příklady na procvičení:

1) 2x . 3 =

2) 15a . 3a² =

3) 2 . x . x . x =

4) 5y . 3y² =

5) 4x . (-2y²) . 5z =

6) - 2a³ . (-5a²) . (-a) =

7) 4 . (5 - x) =

8) (10 + x²) . 3 =

9) 4a (a - 3) =

10) (5ab + 6) . 2a =

11) -11y (5 + y) =

12) (5x - 2) . (-5x) =

13) (x + 2) . (x -12) =

14 (y + 3) . (5 - y) =

15) (2i - 3) . (5i + 8) =

16) (4x + 9) . (2x - 1) =

17) (14 + y)² =

18) (x - 5)² =

19) (11 - a)² =

20) (8x + 4y)² =

21) (5x - 2) (5x + 2) =

22) (3 + 2a) (3 - 2a) =

23) (i² - 4) (i² + 4) =

24) 10 + (3 + x)² =

25) (y - 2)² - 5x =

26) (x + 1)² + (2 - x) . (x + 5) =

27) (11 - a) (11 + a) - (a - 3)² =

28) 15 - (5 + x)² =

29) 10x + 3 . [2 . (5 + x) - 9] =

30) [2 . (3 - y) - (1 + y) (2 - y)] + 5y - 2 =